

Lets start with the trigonometric triangle area formula: area (1/2) × a × b × sin (), where is the angle between the sides. And we use that information and the Pythagorean Theorem to solve for x. Substituting h into the first area formula, we obtain the equation for the equilateral triangle area: area a² × 3 / 4. So this is x over two and this is x over two. Two congruent right triangles and so it also splits this base into two. So the key of realization here is isosceles triangle, the altitudes splits it into
Base of isosceles triangle calculator plus#
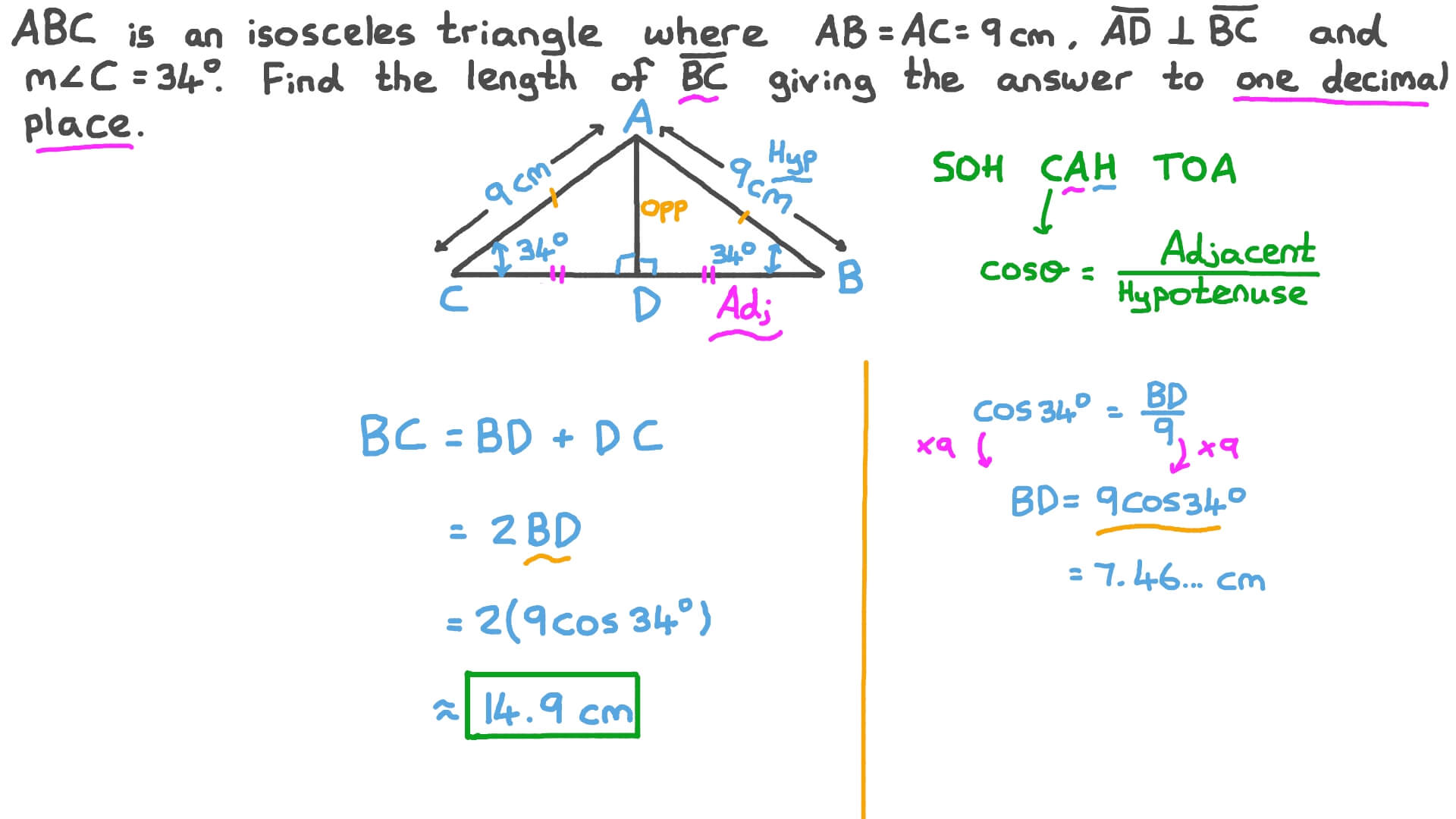
So this length right over here, that's going to be five and indeed, five squared plus 12 squared, that's 25 plus 144 is 169, 13 squared. This distance right here, the whole thing, the whole thing is So x is equal to the principle root of 100 which is equal to positive 10. But since we're dealing with distances, we know that we want the This purely mathematically and say, x could be Is equal to 25 times four is equal to 100. We can multiply both sides by four to isolate the x squared. We calculate alpha sine in the two triangles whose vertices are represented by blue and red points, sin(\alpha) k/b h/a We replace h using the formula above. So subtracting 144 from both sides and what do we get? On the left hand side, we have x squared over four is equal to 169 minus 144. These are the heights from the two ends the isosceles triangle base (length k on the diagram). That's just x squared over two squared plus 144 144 is equal to 13 squared is 169. This is just the Pythagorean Theorem now. We can write that x over two squared plus the other side plus 12 squared is going to be equal to Triangle Calculator Pythagorean Theorem Calculator Right triangle A right triangle is a type of triangle that has one angle that measures 90°. We can say that x over two squared that's the base right over here this side right over here.
Base of isosceles triangle calculator free#
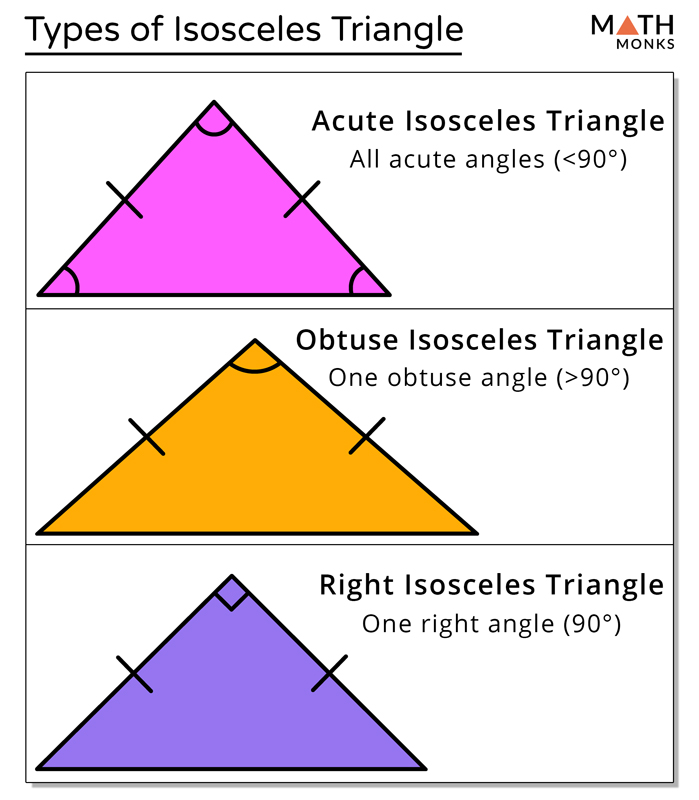
base of an isosceles triangle calculatorIsosceles Triangle Calculator - Free Online Calculator - BYJUS. Let's use the Pythagorean Theorem on this right triangle on the right hand side. base of an isosceles triangle calculator. And so now we can use that information and the fact and the Pythagorean Theorem to solve for x. The general formula that can be used to calculate the area of an isosceles triangle using height is A. So this is going to be x over two and this is going to be x over two. So they're both going to have 13 they're going to have one side that's 13, one side that is 12 and so this and this side are going to be the same. And since you have twoĪngles that are the same and you have a side between them that is the same this altitude of 12 is on both triangles, we know that both of these So that is going to be the same as that right over there. Because it's an isosceles triangle, this 90 degrees is the Is an isosceles triangle, we're going to have twoĪngles that are the same. Well the key realization to solve this is to realize that thisĪltitude that they dropped, this is going to form a right angle here and a right angle here and notice, both of these triangles, because this whole thing "Isosceles Triangle.To find the value of x in the isosceles triangle shown below.

a and b are known find c, P, s, K, ha, hb, and hcįor more information on right triangles see:.To calculate the properties of an isosceles triangle when given certain information, you can use the Pythagorean theorem, the Law of Cosines, or the Law of Sines.
An isosceles triangle is a triangle where two sides have the same length. Given sides a and b find side c and the perimeter, semiperimeter, area and altitudes This calculator calculates any isosceles triangle specified by two of its properties. Altitude c of Isosceles Triangle: hc = (b/2a) * √(4a 2 - b 2).Altitude b of Isosceles Triangle: hb = (1/2) * √(4a 2 - b 2).Altitude a of Isosceles Triangle: ha = (b/2a) * √(4a 2 - b 2).Area of Isosceles Triangle: K = (b/4) * √(4a 2 - b 2).Semiperimeter of Isosceles Triangle: s = (a + b + c) / 2 = a + (b/2).Perimeter of Isosceles Triangle: P = a + b + c = 2a + b.Altitudes of Isosceles Triangle: ha = hc.Let us know if you have any other suggestions! Formulas and Calculations for an isosceles triangle: Once we know sides a, b, and c we can calculate the perimeter = P, the semiperimeter = s, the area = K, and the altitudes: For example, if we know a and b we know c since c = a. In our calculations for a right triangle we only consider 2 known sides to calculate the other 7 unknowns. Triangle where 2 sides, a and c, are equal and 2 angles, A and C, are equal. Calculator UseĪn isosceles triangle is a special case of a *Length units are for your reference only since the value of the resulting lengths will always be the same no matter what the units are.


 0 kommentar(er)
0 kommentar(er)
